Multivariate Regression with Gross Errors on Manifold-valued Data

Multivariate Regression with Gross Errors
on Manifold-valued Data

Xiaowei Zhang (BII), Li Cheng (BII, NUS), Shudong Shi (NUS), Yu Sun (NUS),

  • Abstract

    • We consider the topic of multivariate regression on manifold-valued output, that is, for a multivariate observation, its output response lies on a manifold. Moreover, we propose a new regression model to deal with the presence of grossly corrupted manifold-valued responses, a bottleneck issue commonly encountered in practical scenarios. Our model first takes a correction step on the grossly corrupted responses via geodesic curves on the manifold, and then performs multivariate linear regression on the corrected data. This results in a nonconvex and nonsmooth optimization problem on manifolds. To this end, we propose a dedicated approach named PALMR, by utilizing and extending the proximal alternating linearized minimization techniques. Theoretically, we investigate its convergence property, where it is shown to converge to a critical point under mild conditions. Empirically, we test our model on both synthetic and real diffusion tensor imaging data, and show that our model outperforms other multivariate regression models when manifold-valued responses contain gross errors, and is effective in identifying gross errors.

  • Our Approach

    • Our main idea can be summarized as follows: For each manifold-valued response $\bs{y} \in \mathcal{M}$, we explicitly model its possible gross error (in $\bs{y}$). This gives rise to a \emph{corrected} manifold-valued data $\bs{y}^c$ by removing the identified gross error component from $\bs{y}$, which is realized via geodesic curves on $\mathcal{M}$. Note that $\bs{y}^c$ could be the same as $\bs{y}$, corresponding to no gross error in $\bs{y}$. Then the corrected manifold-valued data can be utilized as the responses in multivariate geodesic regression.

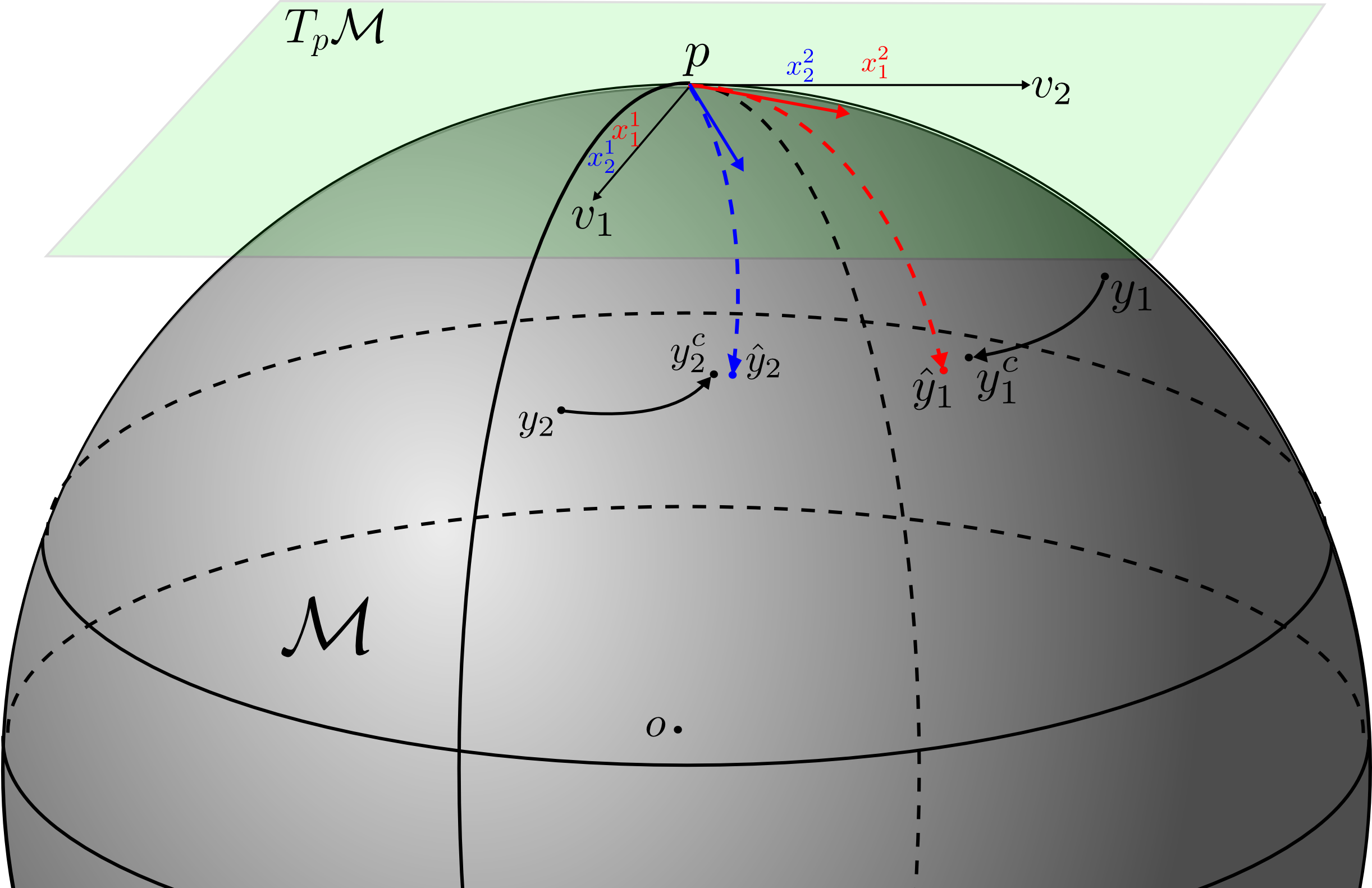
    Illustration of our approach.
    Figure 1: Illustration of our approach, which consists of two main components: First is to obtain the corrected response $\bs{y}_i^c$ by removing its possible gross error, as illustrated by the directed lines; The second one involve the remaining manifold-valued regression process. Here $x_1^1$ and $x_1^2$ are the components of input $\bs{x}_1$ along tangent vectors $\bs{v}_1$ and $\bs{v}_1$ of point $\bs{p}\in\mathcal{M}$. Similarly for $x_2^1$ and $x_2^2$.

  • Publications

    1. Xiaowei Zhang, Li Cheng, Shudong Shi and Yu Sun. Multivariate Regression with Gross Errors on Manifold-valued Data. arXiv:1703.08772, 2017. [pdf]

  • Acknowledgement

    1. The C-MIND dataset used in our experiments contains only six slices of the whole brain DTI data which are obtained from the C-MIND database released by Cincinnati Children's Hospital Medical Center (CCHMC). We do not claim any ownership or credit of the dataset except that we format the data into .mat format.
    2. In our MATLAB code, we also include the implementation of a comparison method (named MGLM in our manuscript), for the sake of easy comparison. The implementation is from the authors of MGLM available here.